 Ruchomy model przekładni korbowej (90kB).
Ruchomy model przekładni korbowej (90kB).
Kinetyka: [Równania ruchu korby] [Równania ruchu krzyżulca (tłoka)] Dynamika: [Rozkład sił] [Punkty martwe] [Maksimum siły obrotowej]
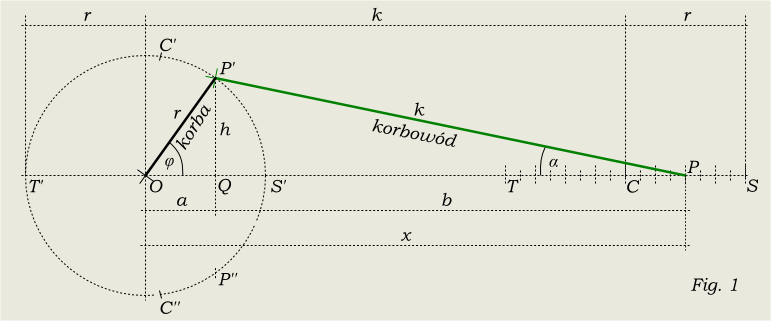 Schemat działania przekładni korbowej
Schemat działania przekładni korbowej
Przekładnia korbowa (ang. crank mechanism, fr. système bielle-manivelle, nm. Kurbeltrieb) zaliczana jest do maszyn prostych ze względu na prostotę jej konstrukcji. Jednakowoż po analizie jej ruchu można się temu dziwić, gdyż mimo prostoty konstrukcji ruch jej części wcale prosty nie jest. Przekładnia służy do zamiany ruchu posuwisto-zwrotnego na ruch obrotowy i odwrotnie. W silnikach różnego rodzaju napędzany tłok przesuwa za pomocą sztywnego trzonu zwanego tłoczyskiem krzyżulec łączący tłoczysko z korbowodem. W maszynach parowych tłok napędzany jest rozprężającą się parą z kotła, w silnikach spalinowych spalinami wytworzynymi podczas spalania paliwa. Przekładni można też używać odwrotnie, jak to ma miejsce w pompach. Wówczas za pomocą silnika np. elektrycznego napędzane jest koło zamachowe a wraz z nim korba, która poprzez korbowód porusza tłoczyskiem a wraz z nim tłokiem, który spręża powietrze w cylindrze lub pompuje wodę.
Matematyczny model przekładni korbowej przedstawia Fig. 1. Odcinek OP' to korba (ang. crank, fr. manivelle, nm. kurbel). Jej długość wynosi r. Odcinek PP' to korbowód (ang. connecting rod, fr. bielle, nm. Pleuelstange) i jego długość wynosi k. Punkt P to krzyżulec (ang. crosshead, fr. crosse, nm. Kreuzkopf), czyli miejsce połączenia trzonu tłoka z korbowodem. Punkt ten porusza się tam i z powrotem po odcinku ST. Punkt P' to czop korbowodu i porusza się on po okręgu o środku w punkcie O (będącym osią korby) i promieniu równym długości korby r. Model przekładni w ruchu pokazuje animacja (90kB).
Ponieważ krzyżulec (punkt P) jest zakończeniem trzonu tłoka (czego rysunek nie pokazuje), to jego położenie odpowiada ustawieniu tłoka w cylindrze. Jak krzyżulec jest w punkcie S to tłok jest w skrajnym prawym końcu cylindra, jak krzyżulec jest w punkcie C to tłok jest dokładnie w środku cylindra, itd. Ponieważ niniejszy opis przekładni korbowej ma na celu dokładniejsze poznanie zasad działania silników parowych, dlatego też często zamiast pisać precyzyjnie "położenie krzyżulca" będę zamiennie używał określenia "położenie tłoka". Mam nadzieję, że czytelnikowi niezainteresowanemu parowozami, a chcącemu bliżej poznać mechanizm przekładni korbowej z innych względów nie utrudni to zrozumienia tekstu. Wnioski bowiem dotyczą każdej przekładni korbowej, niezależnie od jej zastosowania.
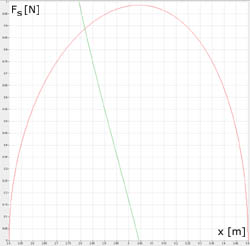
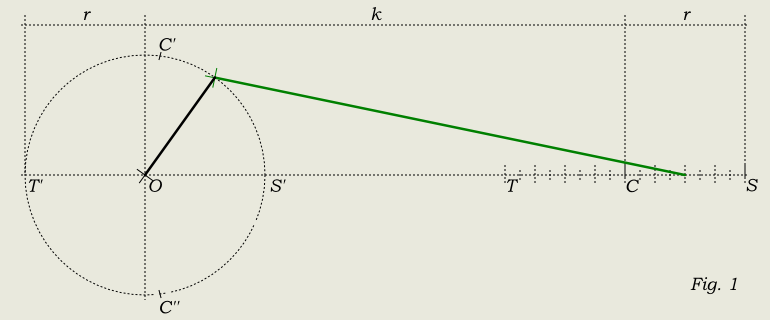
Prostota konstrukcji mechanizmu powoduje, że jego ruch wydaje się być równie nieskomplikowany. Wydaje się, że jeśli będziemy jednostajnie przesuwać krzyżulec (punkt P) po odcinku ST, to czop korbowodu (punkt P') będzie się jednostajnie przemieszczał po okręgu. Gdyby tak było, to w momencie gdy punkt P przebył połowę swojej drogi w lewo i znajduje się w punkcie C wówczas punkt P' powinien przebyć ćwierć okręgu i znajdować się w swoim najwyższym położeniu. Widok większości rzeczywistych konstrukcji może sprawiać takie wrażenie, gdyż zawsze korbowód jest znacznie dłuższy od korby. Jeśli jednak odłożymy cyrklem odległość k od punktu C to otrzymamy na okręgu punkt C', który wcale nie jest najwyżej położony! W momencie gdy tłok znajduje się dokładnie w środku cylindra korba wcale NIE jest ustawiona pod kątem prostym do osi x, gdyż jednostajny ruch tłoka powoduje niejednostajny obrót korby. Zostanie to wykazane w punkcie [Równania ruchu korby]. Niejednostajność tę pokazuje wykres (1), na którym kolorem zielonym oznaczono pożądany, a czerownym rzeczywisty kąt wychylenia korby.
Zadziwiające jest, że wielu autorów rysunków maszyn nie zdaje sobie z tego sprawy lub nie przywiązuje do tego wagi. Na wielu rysunkach technicznych przedstawiających różne maszyny znalazłem błędnie narysowany korbowód, którego czop jest w szczytowym punkcie okręgu, a tłok dokładnie w środku cylindra. Dla czytelnika, który nie analizował ruchu przekładni korbowej jest to często duże utrudnienie w zrozumieniu działania danej maszyny. Sprostowanie tego błędu było jednym z powodów, dla których powstał niniejszy artykuł.
Mechanizm korbowy ma dwa punkty "osobliwe". Są to punkty T i S i nazywa się je punktami martwymi. Nazwa pochodzi stąd, że jeśli krzyżulec (punkt P) zatrzyma się w punkcie S lub T, to mechanizmu nie da się uruchomić ponownie za pomocą siły przyłożonej przez tłok do krzyżulca. Trzeba wtedy przestawić korbę o niewielki nawet kąt za pomocą jakiegoś zewnętrznego mechanizmu rozruchowego, aby siła przyłożona do krzyżulca mogła wprawić korbę w ruch. Dzieje się tak dlatego, że gdy czop korbowodu (punkt P') znajduje się w punkcie S' lub T' to składowa siły wywieranej przez korbowód na czop styczna do okręgu jest zerowa, co zostanie wykazane w rozdziale [Punkty martwe].


Równania ruchu korby przekładni korbowej
Zakładamy, że krzyżulec jest poruszany ruchem jednostajnym. Jego prędkość jest stała: v=const., a położenie zmienia się liniowo x=k+r-vt. Chcemy policzyć równania ruchu korby: jej położenie wyrażone za pomocą kąta φ, prędkość kątową ω i przyspieszenie kątowe ε. Wszystkie w funkcji czasu.
Najpierw policzymy jak zmienia się kąt obrotu korby φ w zależności od
położenia krzyżulca x.
Z twierdzenia Carnota dla trójkąta POP' mamy:
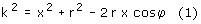
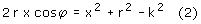
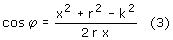
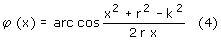
Zależność (4) pokazuje wykres (1), na
którym oznaczono ją kolorem czerwonym, podczas gdy linia zielona pokazuje
jak wyglądałaby ta zależność, gdyby zmiana kąta φ była wprost proporcjonalna
do zmiany położenia tłoka (φ(x)=-Πx+k+r), czyli gdyby przemieszczenie
tłoka o jakąś stałą wartość np. o 10 cm powodowało zawsze identyczny obrót korby
np. o 15°. Jak widać tak niestety nie jest.
Mając zależność kąta obrotu korby od położenia krzyżulca, łatwo sprawdzimy pod jakim
kątem będzie ustawiona korba w momencie gdy tłok osiągnie położenie centralne C, dokładnie w
środku cylindra. Do powyższego wzoru wstawiamy x=k i otrzymujemy:
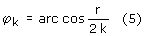
Ponieważ cos 90°=0 więc aby kąt φk wynosił 90° potrzeba by r/2k=0, co zachodzi
dla r=0, a to oznacza brak korby (oś korby połączona bezpośrednio z trzonem tłoka)
oraz dla k=∞ czyli nieskończenie długiego korbowodu.
Zatem niezależnie od długości korby i korbowodu w momencie gdy tłok znajduje się dokładnie w
środku cylindra korba NIE jest ustawiona pod kątem prostym! Kąt ten jest ostry i tym bardziej
zbliżony do kąta prostego im dłuższy jest korbowód i im krótsza korba.
Założyliśmy, że położenie krzyżulca x zmienia się ze stałą prędkością v.
W chwili t0=0 krzyżulec znajduje się w skrajnym prawym położeniu S,
jego wychylenie jest wówczas maksymalne i wynosi x0=k+r.
Wychylenie minimalne xmin=k-r nastąpi w momencie kiedy krzyżulec
osiągnie skrajne lewe położenie T. Zatem zależność
położenia krzyżulca od czasu wyraża się wzorem:
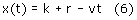
Pochodna położenia krzyżulca, czyli jego prędkość jest zgodnie z
założeniem stała i wynosi:
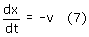
Wstawiając (6) do (4) otrzymujemy kąt obrotu korby φ w zależności od czasu
t:
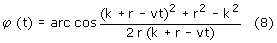
Prędkość kątowa korby ω jest pierwszą pochodną kąta φ względem czasu:
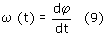
Aby ją obliczyć skorzystamy z kilku zależności znanych z rachunku róźniczkowego.
Pochodna funkcji f(x)=xn:
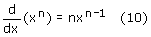
Pochodna funkcji f(x)=arc cos x:
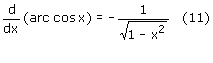
Pochodna funkcji złożonej y = f(x(t)):
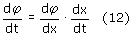
Pochodna iloczynu dwóch funkcji:
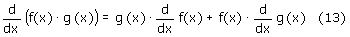
Stosując powyższe zależności otrzymujemy:
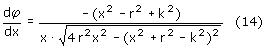
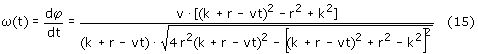
Zauważmy, że aby ruch obrotowy korby był jednostajny musiałoby być ω(t) = const.,
zatem w powyższym wzorze (15) czas t w ogóle by nie występował. Niestety tak nie jest.
Przyspieszenie kątowe korby ε jest pochodną jej prędkości kątowej po
czasie, czyli drugą pochodną kąta po czasie.
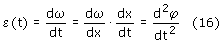
Aby je obliczyć różniczkujemy więc prędkość kątową po x i mnożymy przez pochodną
x względem t z równania (7).
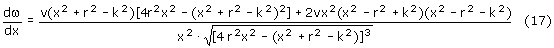
Ostatecznie przyspieszenie kątowe wyraża się wzorem:
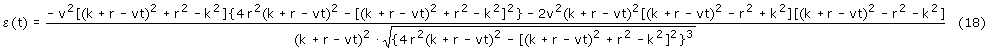
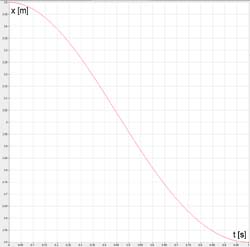
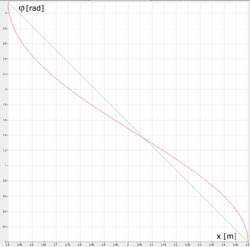 Wykres (1). Kąt odchylenia korby φ w funkcji położenia krzyżulca przy r=0.5 m, k=3 m.
Wykres (1). Kąt odchylenia korby φ w funkcji położenia krzyżulca przy r=0.5 m, k=3 m.
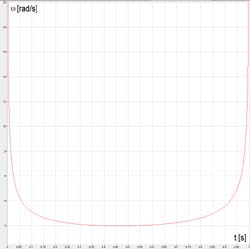
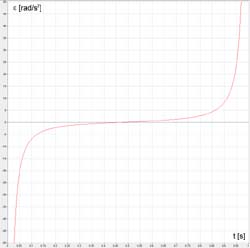
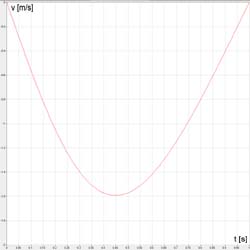
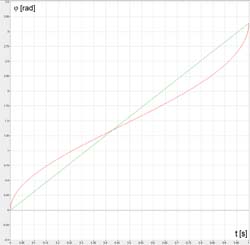 Wykres (2). Kąt odchylenia korby φ w funkcji czasu przy r=0.5 m, k=3 m, v=1
m/s.
Wykres (2). Kąt odchylenia korby φ w funkcji czasu przy r=0.5 m, k=3 m, v=1
m/s.
Równania ruchu krzyżulca (tłoka) przekładni korbowej
Zakładamy, że korba jest poruszana jednostajnym ruchem obrotowym. Oznacza to, że jej prędkość kątowa jest stała: ω(t)=const., a kąt zmienia się liniowo: φ(t)=ωt. Chcemy policzyć równania ruchu krzyżulca: jego pozycję x, prędkość v i przyspieszenie a - w funkcji czasu.
Z twierdzenia Pitagorasa dla trójkątów QOP' i QPP' mamy:
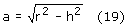
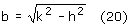
Z definicji sinusa dla kąta φ:
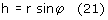
Zatem:
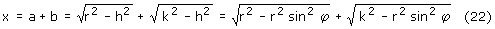
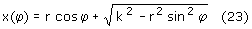
Wstawiamy φ=ωt do (23) i otrzymujemy zależność położenia krzyżulca od czasu:
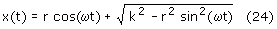
Stosując wcześniej podane zależności rachunku różniczkowego oraz dodatkowo w
wiedząc, że pochodna sinusa sin(x)'=cos(x), a pochodna cosinusa cos(x)'=-sin(x) otrzymujemy
wzór na prędkość krzyżulca v(t):
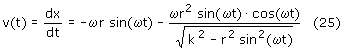
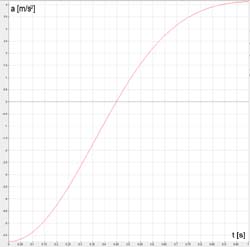
Różniczkując prędkość v z równania (25) po czasie dostaniemy przyspieszenie
krzyżulca a(t):
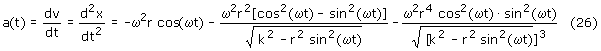
Rozkład sił w przekładni korbowej
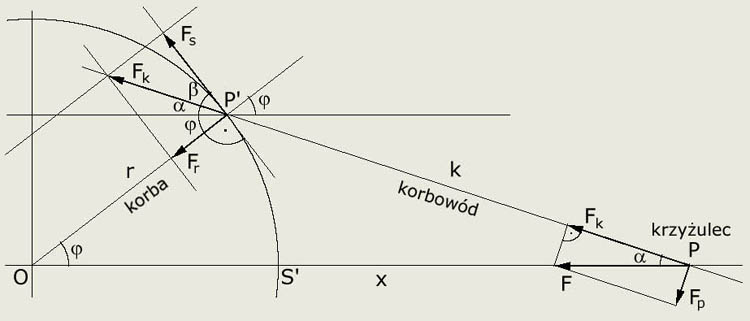
Rys.(2). Rozkład sił w przekładni korbowej.
Do krzyżulca przyłożona jest stała pozioma siła F. Siłę tę wywiera na niego tłok za pośrednictwem tłoczyska. Obrót korby powoduje natomiast siła Fs, która jest przyłożona w punkcie P' (czop korbowodu) i jest styczna do okręgu zataczanego przez korbę. Chcemy wiedzieć jak wielkość tej siły zmienia się w zależności od położenia krzyżulca, czyli od x.
Z twierdzenia sinusów dla trójkąta dowolnego mamy:
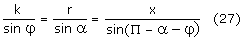
Z własności funkcji trygonometrycznych wiemy, że dla każdego kąta A zachodzi
zależność:
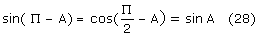
Przekształcając (27) z uwzględnieniem (28) mamy:
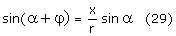
Z rysunku widać, że:
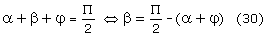
z czego, uwzględniając (28) otrzymamy:
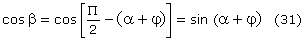
Z definicji cosinusa mamy zależności:
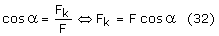
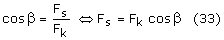
Wstawiamy (32) do (33), do wyniku wstawiamy (31), a następnie (29) i
otrzymujemy:
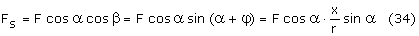
Z twierdzenia Carnota dla trójkąta dowolnego mamy:
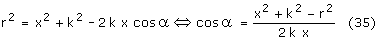
a z jedynki trygonometrycznej:
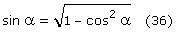
Wstawiamy teraz (35) i (36) do (34) i otrzymujemy wartość Fs w funkcji x:
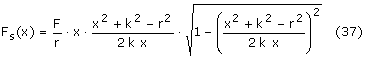
Upraszczając (37) mamy w końcu wzór na siłę styczną do okręgu Fs w funkcji położenia krzyżulca x:
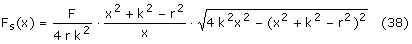
Cóż, jak na maszynę prostą to niezły wynik. Pchamy sobie tłok ze stałą siłą F
i to jest tak jakbyśmy kręcili kołem z siłą Fs, która nie dość, że nie
jest stała to jeszcze zależy od tego w którym akurat miejscu jest tłok i to nie
jakoś tam proporcjonalnie, czy logarytmicznie, ale w sposób wyrażony raczej
pokręconym wzorem (38). Prostota, umiar, elegancja. W jaki sposób "krzywa" jest
ta zależność pokazuje wykres (7). Nigdzie w
literaturze technicznej nie spotkałem się z określeniem "krzywa korbowa", ale wydaje się,
że właśnie tak należałoby ją nazwać.
Punkty martwe
Zobaczmy, kiedy nasz wysiłek idzie na marne, tj. kiedy korba się nie zakręci pomimo, że pchamy
tłok i to nieważne jak mocno (wartość F jest dowolna). Innymi słowy policzymy miejsca zerowe
funkcji Fs(x). Zauważmy, że prawa strona wzoru (37) przyjmuje wartość 0 wtedy gdy
wyrażenie pod pierwiastkiem przyjmuje wartość 0, a to z kolei ma miejsce tylko gdy licznik
ułamka pod pierwiastkiem jest równy jego mianownikowi.
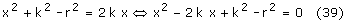
Rozwiązujemy równanie kwadratowe:
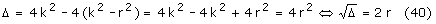
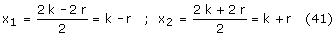
Mamy więc dwa punkty martwe: x=k-r (wówczas krzyżulec P znajduje się w punkcie T)
oraz x=k+r (krzyżulec w punkcie S).
Dla porządku wspomnieć należy, że oprócz punktów x1 i x2 Fs(x) również będzie równa 0 w punkcie, w którym licznik pierwszego ułamka we wzorze (37) jest równy 0. Ale to ma miejsce dla x2=r2-k2, co przy korbowodzie dłuższym od korby (r < k) nie zachodzi nigdy (r2 < k 2 czyli r2-k 2<0 zatem x2 musiałoby być ujemne).
Maksimum siły obrotowej
Żeby wyliczyć te punkty x, w których siła Fs jest maksymalna i znaleźć jej
wartość należy zróżniczkować funkcję Fs(x) po x i znaleźć miejsca
zerowe tej pochodnej. Korzystając ze wzorów (10)-(13) i starając się liczyć
powoli i uwaznie żeby nie popełnić błędu otrzymujemy wzór na pochodną:
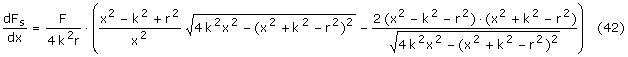
Pozostaje tylko znaleźć miejsca zerowe powyższej funkcji. Łatwo zauważymy, że
aby pochodna było równa 0 wyrażenie w nawiasie musi być równe 0, a to zachodzi
gdy jego część przed minusem jest równa ułamkowi po minusie:
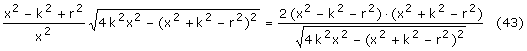
Obie strony mnożymy przez x2 razy pierwiastek z mianownika strony
prawej, pozbywając się pierwiastków i ułamków po obu stronach:
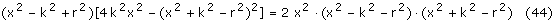
Zauważmy, że x, k, r występują wszędzie w kwadratach, więc dla uproszczenia zastosujemy
podstawienia X=x2, K=k2, R=r2, co pozwoli zredukować
równanie dwusześcienne do sześciennego.
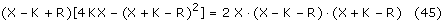
Teraz trzeba wymnożyć, przenieść na lewą stronę i uprządkować wyrazy podobne, co jest
zadaniem bardzo żmudnym zważywszy na ilość czynników i liczyć na szczęście, że wiele wyrazów
zredukuje się do zera. Niestety się nie zredukowało i otrzymujemy następujące równanie:
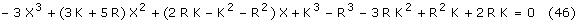
Jest to równanie sześcienne, które ma przynajmniej jeden pierwiastek rzeczywisty i da się go znaleźć. Należałoby sprowadzić równanie do postaci kanonicznej, czyli wyrugować czynnik z X2, a następnie rozwiązać równanie kanoniczne metodą Cardano. Biorąc jednak pod uwagę, że współczynniki przy X w poszczególnych potęgach są dość złożone, a kształt wyrazu wolnego (który podczas obliczeń znajdzie się w mianowniku) przekracza moje pojmowanie prostoty, nie będę tego liczył. Czytelnik musi się zadowolić informacją, że maksimum siły obrotowej istnieje. Punkt x, w którym siła Fs jest największa można określić rozwiązując równanie (46) ze względu na X, następnie wynik należy spierwiastkować bo jak pamiętamy podstawiliśmy X=x2, a potem należy otrzymaną wartość wstawić do równania (38) i w ten sposób otrzymamy wzór na maksymalną wartość siły Fs. Będzie to plątanina ułamków, pierwiastków trzeciego i drugiego stopnia oraz potęg (od pierwszej do szóstej włącznie) z udziałem r, k i wielu stałych. Prostota, umiar, elegancja - jak na maszynę prostą przystało. Pocieszający jest jedynie fakt, że dla konkretnych wartości r i k obliczenia byłyby szybsze, gdyż wszystkie współczynniki wyliczalibyśmy ad hoc, więc każdy współczynnik miałyby postać jednej konkretnej liczby.
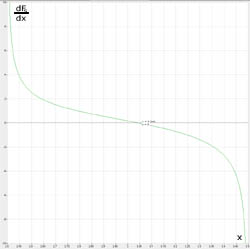
Póki co można obejrzeć wykres (8), który przedstawia zależność Fs(x) [czerwony - równanie (38)] i dFs/dx [zielony - równanie (42)] dla konkretnych wartości r=0.5 m, k=3 m i F=1 N. Widać na nim, że maksymalna wartość Fs istnieje, wynosi prawie tyle samo ile siła, z którą pchamy tłok, a znajduje się w punkcie w którym pochodna (zielona) przecina oś x - kiedy tłok osiągnie położenie niedaleko przed środkiem cylindra.
Wygląda na to, że jest to punkt, w którym korbowód jest styczny do okręgu, a więc prostopadły
do korby (x odpowiadający sytuacji gdy czop korbowodu P' znajduje się w punkcie C' na
rys.(1)).
Sprawdzimy czy rzeczywiście tak jest. W tym położeniu trójkąt OPP' jest
prostokątny więc z twierdzenia Pitagorasa mamy
x2=k2+r2. Zobaczmy czy dla tak dobranego x równanie (42)
przyjmie wartość 0. Wstawiamy do (42) x2=k2+r2 i otrzymujemy:
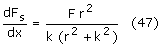
czyli... wartość różną od 0. Niestety maksimum siły obrotowej NIE występuje gdy
korbowód jest prostopadły do korby. Ewidentnie byłoby to zbyt proste.